Los alumnos de 4ºESO de Ampliación nos ayudan a resolver los ejercicios de demostraciones utilizando el principio de inducción. Blanca nos resuelve el ejercicio 9:
EJERCICIO 9:
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² = 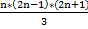
1º - Simplificamos la ecuación de la derecha de la igualdad, para simplificar los cálculos.
Vemos que en el numerador hay una ecuación del tipo (a+ b)*(a-b), sabemos que es una igualdad notable que es igual a (a²+b²). Sustituimos por este valor y realizamos la operación para que quede más reducido.
![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiqwNFev53-5zapLvNzuL5GH_8dmLkt4jqICP8DLW4qBJwhQ87e3N_evhvrOr-QgTFu-n13sFByeFyBTA0PKpfZvfOp80CIqlOjbbavVT3ow9V2sDbsUU6SgWXLCb_T5-9V_jOze0VBeq_5/?imgmax=800) =
= 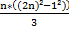 =
=  =
= 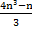
Con lo que la ecuación nos queda de la siguiente forma:
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² = ![clip_image008[1] clip_image008[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjHbe3bNdLRsi2rKI-w4ookj8sbx0loPV4buTS2GnzXcMUwLimPs_FAU33QDWYR7s19w-qjq0xASidelIEeGic2wN8kyQzZ42heljkhkUThNNBusx3wDraiy7sDj4m2b4ZLWgixJF5G0owx/?imgmax=800)
2º - Comprobamos que la ecuación se cumple para distintos valores de ‘n’.
 n = 1
n = 1
Como ‘n’ es igual a 1, nos quedamos sólo con ‘a₁’. Es decir, sólo el primer término de la sucesión.
Y en el otro lado de la igualdad, sustituimos el valor de la ‘n’ por 1.
1² = 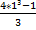 ; 1² =
; 1² = 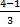 ; 1² =
; 1² =  ; 1 = 1
; 1 = 1
Vemos que se cumple la ecuación para ‘n=1’.
Vamos a comprobar si se cumple para ‘n=2’.
 n = 2
n = 2
Tomamos los 2 primeros términos de la sucesión ‘a₁’ y ‘a₂’ y vamos a comprobar si su suma es igual al resultado de sustituir la ‘n’ por ‘2’ en la ecuación del otro lado de la igualdad.
1² + 3² = 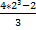 ; 1² + 3² =
; 1² + 3² = 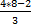 ; 1 + 9 =
; 1 + 9 = 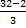 ; 10 =
; 10 =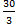 ; 10 = 10
; 10 = 10
Vemos que también se cumple la ecuación para ‘n=2’.
Seguimos con las comprobaciones y vamos a probar si se cumple para ‘n=3’.
![clip_image016[1] clip_image016[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjkIaJio3dINtf7wqHH8ht0Exi0mm0VO19wUJ6MBqZ12a0M4Mb0dSh6J6Bu71c7ABuP7ywPYew28TUZM9SQr8GAWk4ejrmRtFhUY1-eSKG-HceRnTqqPKqww7UNQecXcRc8tjR5OsKeOG1e/?imgmax=800) n = 3
n = 3
Tomamos los 3 primeros términos de la sucesión ‘a₁’, ‘a₂’ y ‘a₃’ y vamos a comprobar si su suma es igual al resultado de sustituir la ‘n’ por ‘3’ en la ecuación del otro lado de la igualdad.
1² + 3² + 5² = 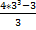 ; 1 + 9 + 25 =
; 1 + 9 + 25 = 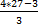 ; 35 =
; 35 = 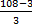 ; 35 =
; 35 =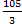 ; 35 = 35
; 35 = 35
También se cumple la ecuación para ‘n=3’.
3º - Realizamos una hipótesis sobre el cumplimiento de la ecuación para ‘n’.
Podríamos seguir probando con los distintos valores de ‘n’, pero si se ha cumplido para n=1, n=2 y n=3, podemos suponer que se cumple para ‘n’.
4º - Comprobamos si la ecuación también se cumple para valores mayores que ‘n’ y para ello vamos a probarlo con ‘n+1’.
En uno de los lados de la igualdad tenemos una suma de ‘n’ números impares al cuadrado. Para realizar la comprobación con ‘n+1’ tenemos que añadir un sumando más, que será el resultado de sustituir en el último término (2n-1) ² el valor de la ‘n’ por ‘n+1’.
En el otro lado de la igualdad, tenemos una ecuación donde hay que sustituir el valor de ‘n’ por ‘n+1’.
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² + (2(n+1)-1)² = 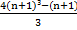
Realizamos operaciones en cada lado de la igualdad para reducir al máximo las expresiones.
Primero quitamos los paréntesis internos:
![clip_image008[3] clip_image008[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUrJv-HtIPnLbN75xD2hmzkfkoDXj13RfKxvS378r9UjD09k1XckTH9deDj_wvD_fBQYq-cw5qxGQ6F0w-1A48sosZ_NzCifckshhKevtMrYI8Abd3VMfYDYsBCbpCSZ5_xrZb312uamip/?imgmax=800) + (2n+2-1)² =
+ (2n+2-1)² = ![clip_image037[2] clip_image037[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgsuO3DNobzFXiRztYut66PoAWIgn7SFbXSUZQRd_Xw5GMSUFIwTdQcW0M9AGpyLXnaIKlXx3MDyN020mc9dU_IlfUphCLXa6EEfWlBztBNfp9hMcXiXU2Jj64E0qIgGkpbYMjZe5ALJ5pI/?imgmax=800)
Seguimos operando para eliminar todos los paréntesis:
![clip_image008[4] clip_image008[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj9E53OR3JBQgjSTrUv1haH5eT6iJce3x9kOVEwa9um3xOpbJhSLsiKObllbxNavETO67Vjlz4THlfQ5slQ2AzQpAVZXhJ_cvvV8tRFelc0tkhyZcVXPjLsymAUTlwoNjAS0a-kPwxdVshR/?imgmax=800) + (2n+1)² =
+ (2n+1)² = 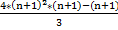 ;
;
 Aplicamos la igualdad notable (a + b)²= a²+2ab+b:
Aplicamos la igualdad notable (a + b)²= a²+2ab+b:

![clip_image008[5] clip_image008[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg0nVI89HHRYghNMxqtZ3kHtpwZ5JYAKeNKibFaPbJ3nkGxOKcgFi8DysILpkM-x7r_PxDE_UvZf9ffLWHMC9AjKo7-QpY_wuU68mSRbvT7nD7XaFv54dbtdb5Fg723YB_r_fBwyGhf0cI4/?imgmax=800) + (4n²+4n+1) =
+ (4n²+4n+1) = 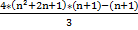
| 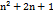
x n + 1 n² + 2n + 1 n³ + 2n² + n ……. n³ + 3n² + 3n + 1 | |
Realizamos la multiplicación
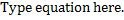
Sustituimos el resultado y seguimos operando.
![clip_image008[6] clip_image008[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiKwpOet-IlY2O0kWSUUq860IMKwHyJZntQl5glrk3T612tjhwnKRuHrH_WiGhGapd7toDFNK2W_7frSTR-NEnhAMam8QAvvdtBw33Syy12rhlm5L1Jttu_0kr7N-_V5nCVTOacIhUuEbqD/?imgmax=800) + (4n²+4n+1) =
+ (4n²+4n+1) = 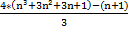
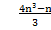 + (4n²+4n+1) =
+ (4n²+4n+1) = 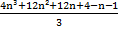
![clip_image054[1] clip_image054[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiU-GlFK1sBXHRpuC1RrvogmYn7colaVevaB0b3l4PLp5Jpiucx9Fg1VLyRk0pqqe-IC64tDcxH0EoHda7TQfC7HLgMII3WowXl2_h65zZvBd2x16n4kAJNtGaLWIrXH3drpiw5SCuckNXZ/?imgmax=800) + (4n²+4n+1) =
+ (4n²+4n+1) = 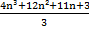
Calculamos el mcm (mínimo común múltiplo) para que todo tenga el mismo denominador y seguimos realizando operaciones.
m.c.m. = 3
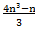 +
+ 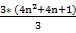 =
= ![clip_image058[1] clip_image058[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhVDcz9a2fMOjwVZNw4ulZzEchO5RHeSsAnHY9xg3rVXVG4ikWFlYknK7JdfKVOc8ae0EII65bnTfGhjyqEzHo2EWKcRB5XpaPiIIaRqRcCR3pBhBOImgNZ37SJ8YjvTs5TttY0fjnQ5XtM/?imgmax=800)
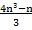 +
+ 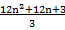 =
= ![clip_image058[2] clip_image058[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhgsQ8cUAUnUejIr8kEuIvP8KMhRC3MrB4nMq6Shyphenhyphenk74i_08_uimNWpF5ET7cNUA7NOY99WjFaZtyiCmD4bQ4uiRPd9az2jbwJvJeJS6LVw09osfJ24OqoDOyyyf74ExdfsqlI1J7u1qDZ1/?imgmax=800)
Hemos comprobado que también se cumple para ‘n+1’.
Por el Principio de la Inducción, podemos asegurar que se cumple la igualdad.
Resuelto por Blanca Minguito.
=
=4 También se cumple. Al sumar los dos primeros números impares, el resultado es igual que
. Al sustituir
por n=2, sería
, que resulta ser 4. Entonces, el resultado de
es igual a la suma de los dos primeros números impares.
se sustituye por 3.
=
=9
= sucesión de nº impares.
=1
=3
=9
, sustituyo y me queda:


