Blog del Departamento de Matemáticas del Colegio Madres Concepcionistas Madrid-Princesa
martes, 28 de octubre de 2014
2º ESO Potencias y fracciones
martes, 14 de octubre de 2014
La magia de los números de Fibonacci
http://www.ted.com/talks/arthur_benjamin_the_magic_of_fibonacci_numbers
¿Por qué es "x" la incógnita?
http://www.ted.com/talks/terry_moore_why_is_x_the_unknown
martes, 9 de septiembre de 2014
EDMODO
Entrar en edmodo:
- www.edmodo.com (si quieres puedes cambiar el idioma en la parte inferior derecha)
Tutoriales:
miércoles, 9 de abril de 2014
Ejercicios 4ºESO Geometría Analítica SEMANA SANTA
Los ejercicios del libro de texto son:
- Página 191: 67, 68, 69 y 70.
- Página 192: 82, 84 y 85.
miércoles, 2 de abril de 2014
Pruebas del CDI
miércoles, 12 de febrero de 2014
Estadística
lunes, 10 de febrero de 2014
Principio de inducción. Ejercicio 12
Alejandro nos resuelve el ejercicio 12
Demuestra que la suma an= es divisible por 133 cualquiera que sea el nº entero n>=0
→
1) Compruebo que da para n=1
3059=133 x p
P=
Compruebo que da para n=2
263473=133 x p
P=1981
2) Supongo que se cumple para cualquier n y demuestro que también para n+1
* 11 – 11*
133p *11 +
133p* 11 +
133p* 11 +
133(p * 11 + )
QUEDA DEMOSTRADO QUE ES MÚLTIPLO.
Resuelto por Alejandro Fernández, 4ºESO B
Principio de inducción. Ejercicio 7
Roberto nos resuelve el problema 7:
7. Demostrar que para cualquier número natural n,la suma de tres números sucesivos elevados al cubo sea divisible entre 9.
Compruebo para n = 1.
13 + 23+ 33 =1+8+27= 36 que es divisible por 9
Y, suponiendo que la propiedad es cierta para r = 1, es decir, que r3+ (r+1) 3+ (n+2) 3 es divisible por 9.
n3 + (n + 1) 3 + (n + 2) 3 = a, a entre 9 es igual a (x) y el resto es igual a 0.
Hay que probar que se cumple para r = r + 1.
(n + 1) 3 + (n + 2) 3+ (n + 3) 3 = (n + 1) 3 + (n + 2) 3 + n3 + 9n2 + 27n + 27 =
= [n3 + (n + 1) 3 + (n + 2) 3] + 9(n2 + 3n + 3) = 9a + 9(n2+ 3n + 3)
Que es múltiplo de 9, y la propiedad es cierta para n = n+1. Entonces, por el principio de inducción Matemática, la propiedad es verdadera para cualquier número natural.
Resuelto por Roberto Alonso, 4ºESO B
sábado, 8 de febrero de 2014
Principio de Inducción. Ejercicio 2
Nacho nos explica como resolver el ejercicio 2
Demostrar que la suma de los cuadrados de los n primeros números naturales es igual a:
1- Demuestro que se cumple para n=1
n=1 1²=1
2- Como suponemos que es verdad comprobamos demostrando con n+1
Iremos por partes:
Empecemos con la parte sin fracción:
Hacemos el mcm (mínimo común múltiplo) de los denominadores que da seis
Resolvemos paréntesis
El resultado de una de las partes de la ecuación es : . vamos a resolver la otra parte de la ecuación y si nos da igual que esta la formula se cumple
Empecemos resolviendo los paréntesis:
Como en el mcm da seis al dividir 6:6 da 1 y el uno lo multiplicamos por toda la expresión
Como da lo mismo se cumple la formula
CQD (como queda demostrado)
Realizado por Nacho Oquillas, 4ºESO C
Principio de Inducción. Ejercicio 1
Miguel nos explica el ejercicio 1:
Demuestra que para cualquier número natural n se cumple que:
1º Comprobamos que se cumple para n=1
2º Suponemos que es verdad paran n y demuestro también es para n+1
↓
↓
↓
↓
C.Q.D (Se cumple)
Realizado por Miguel Ribeiro, 4ºESO B
viernes, 31 de enero de 2014
Principio de inducción. Ejercicio 15
| Noé nos resuelve el ejercicio 15 |
siendo a > 0
1º Compruebo que se cumple para n=1
Sustituimos por n=1, y comprobamos que la inecuación se cumple:
(1+a)^1 ≥ 1+a
1+a ≥ 1+a
y también para n=2
(1+a)2≥1+2a
1+2a + a2≥ 1+2a porque a > 0 así que a^2 > 0
Como se cumple, continuamos con nuestro ejercicio.
2º Suponemos que se cumple para n, y demostramos n+1
Sustituimos las n de la fórmula por n+1 y buscamos una forma de comprobar que se cumple.
- Podemos resolverlo de dos formas:
Procedimiento 1.- La suma en el exponente es igual a un producto con la misma base, así que:
Sabemos que así que tenemos que comparar (1+a) y a. Como por el enunciado a > 0, entonces 1+a>a obligatoriamente.
Por lo que al ser , y (1+a) > a; esto implica que es verdad que
Procedimiento 2.-
Sabemos que , por lo que
(porque al ser
, si multiplicamos un número cualquiera como
en un lado de la inecuación, habrá que hacerlo en el otro.)
· Sacamos factor común a de los dos términos del medio
· , por lo que al ser
mayor o igual que
,
que era mayor o igual que
, va a ser aún mayor o igual que
. De forma que queda demostrado por principio de inducción con n+1.
Resuelto por Noé Carabias, 4ºESO C

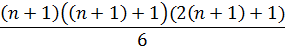

![clip_image002[7] clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjbqnX9EZBOZb8Vq0zg6pSLN2vJ4-iShJ-4Qxm7rXWrWkAF4ReZRuDVdvihkWkjOqNjhVvyNbpvV-JwS-ocyD42Bkp7VPgOwxNoniLZ3dureZLz4XrLOaFD1TBuC4sD5-WjymesROi0Q4pQ/?imgmax=800)
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhDO1w0tZ132DMkjks3-M5K1U8CrazgP0Uy29FdFgf8ZQuG6IF28nMoeOHgxx59jZCakpfWSgHO5LEvraba7g9HZs7Z82mEeQzYwCbmRzmAh1G9YyJyN73nJfYpnHTQGbnRvD4TWw7nukTI/?imgmax=800)