Blog del Departamento de Matemáticas del Colegio Madres Concepcionistas Madrid-Princesa
martes, 28 de octubre de 2014
2º ESO Potencias y fracciones
lunes, 10 de febrero de 2014
Principio de inducción. Ejercicio 12
Alejandro nos resuelve el ejercicio 12
Demuestra que la suma an= es divisible por 133 cualquiera que sea el nº entero n>=0
→
1) Compruebo que da para n=1
3059=133 x p
P=
Compruebo que da para n=2
263473=133 x p
P=1981
2) Supongo que se cumple para cualquier n y demuestro que también para n+1
* 11 – 11*
133p *11 +
133p* 11 +
133p* 11 +
133(p * 11 + )
QUEDA DEMOSTRADO QUE ES MÚLTIPLO.
Resuelto por Alejandro Fernández, 4ºESO B
Principio de inducción. Ejercicio 7
Roberto nos resuelve el problema 7:
7. Demostrar que para cualquier número natural n,la suma de tres números sucesivos elevados al cubo sea divisible entre 9.
Compruebo para n = 1.
13 + 23+ 33 =1+8+27= 36 que es divisible por 9
Y, suponiendo que la propiedad es cierta para r = 1, es decir, que r3+ (r+1) 3+ (n+2) 3 es divisible por 9.
n3 + (n + 1) 3 + (n + 2) 3 = a, a entre 9 es igual a (x) y el resto es igual a 0.
Hay que probar que se cumple para r = r + 1.
(n + 1) 3 + (n + 2) 3+ (n + 3) 3 = (n + 1) 3 + (n + 2) 3 + n3 + 9n2 + 27n + 27 =
= [n3 + (n + 1) 3 + (n + 2) 3] + 9(n2 + 3n + 3) = 9a + 9(n2+ 3n + 3)
Que es múltiplo de 9, y la propiedad es cierta para n = n+1. Entonces, por el principio de inducción Matemática, la propiedad es verdadera para cualquier número natural.
Resuelto por Roberto Alonso, 4ºESO B
sábado, 8 de febrero de 2014
Principio de Inducción. Ejercicio 2
Nacho nos explica como resolver el ejercicio 2
Demostrar que la suma de los cuadrados de los n primeros números naturales es igual a:
1- Demuestro que se cumple para n=1
n=1 1²=1
2- Como suponemos que es verdad comprobamos demostrando con n+1
Iremos por partes:
Empecemos con la parte sin fracción:
Hacemos el mcm (mínimo común múltiplo) de los denominadores que da seis
Resolvemos paréntesis
El resultado de una de las partes de la ecuación es : . vamos a resolver la otra parte de la ecuación y si nos da igual que esta la formula se cumple
Empecemos resolviendo los paréntesis:
Como en el mcm da seis al dividir 6:6 da 1 y el uno lo multiplicamos por toda la expresión
Como da lo mismo se cumple la formula
CQD (como queda demostrado)
Realizado por Nacho Oquillas, 4ºESO C
Principio de Inducción. Ejercicio 1
Miguel nos explica el ejercicio 1:
Demuestra que para cualquier número natural n se cumple que:
1º Comprobamos que se cumple para n=1
2º Suponemos que es verdad paran n y demuestro también es para n+1
↓
↓
↓
↓
C.Q.D (Se cumple)
Realizado por Miguel Ribeiro, 4ºESO B
viernes, 31 de enero de 2014
Principio de inducción. Ejercicio 15
| Noé nos resuelve el ejercicio 15 |
siendo a > 0
1º Compruebo que se cumple para n=1
Sustituimos por n=1, y comprobamos que la inecuación se cumple:
(1+a)^1 ≥ 1+a
1+a ≥ 1+a
y también para n=2
(1+a)2≥1+2a
1+2a + a2≥ 1+2a porque a > 0 así que a^2 > 0
Como se cumple, continuamos con nuestro ejercicio.
2º Suponemos que se cumple para n, y demostramos n+1
Sustituimos las n de la fórmula por n+1 y buscamos una forma de comprobar que se cumple.
- Podemos resolverlo de dos formas:
Procedimiento 1.- La suma en el exponente es igual a un producto con la misma base, así que:
Sabemos que así que tenemos que comparar (1+a) y a. Como por el enunciado a > 0, entonces 1+a>a obligatoriamente.
Por lo que al ser , y (1+a) > a; esto implica que es verdad que
Procedimiento 2.-
Sabemos que , por lo que
(porque al ser
, si multiplicamos un número cualquiera como
en un lado de la inecuación, habrá que hacerlo en el otro.)
· Sacamos factor común a de los dos términos del medio
· , por lo que al ser
mayor o igual que
,
que era mayor o igual que
, va a ser aún mayor o igual que
. De forma que queda demostrado por principio de inducción con n+1.
Resuelto por Noé Carabias, 4ºESO C

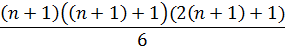

![clip_image002[7] clip_image002[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjbqnX9EZBOZb8Vq0zg6pSLN2vJ4-iShJ-4Qxm7rXWrWkAF4ReZRuDVdvihkWkjOqNjhVvyNbpvV-JwS-ocyD42Bkp7VPgOwxNoniLZ3dureZLz4XrLOaFD1TBuC4sD5-WjymesROi0Q4pQ/?imgmax=800)
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhDO1w0tZ132DMkjks3-M5K1U8CrazgP0Uy29FdFgf8ZQuG6IF28nMoeOHgxx59jZCakpfWSgHO5LEvraba7g9HZs7Z82mEeQzYwCbmRzmAh1G9YyJyN73nJfYpnHTQGbnRvD4TWw7nukTI/?imgmax=800)