Los alumnos de 4ºESO de Ampliación nos ayudan a resolver los ejercicios de demostraciones utilizando el principio de inducción. Blanca nos resuelve el ejercicio 9:
EJERCICIO 9:
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² =
1º - Simplificamos la ecuación de la derecha de la igualdad, para simplificar los cálculos.
Vemos que en el numerador hay una ecuación del tipo (a+ b)*(a-b), sabemos que es una igualdad notable que es igual a (a²+b²). Sustituimos por este valor y realizamos la operación para que quede más reducido.
Con lo que la ecuación nos queda de la siguiente forma:
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² =
2º - Comprobamos que la ecuación se cumple para distintos valores de ‘n’.
Como ‘n’ es igual a 1, nos quedamos sólo con ‘a₁’. Es decir, sólo el primer término de la sucesión.
Y en el otro lado de la igualdad, sustituimos el valor de la ‘n’ por 1.
Vemos que se cumple la ecuación para ‘n=1’.
Vamos a comprobar si se cumple para ‘n=2’.
Tomamos los 2 primeros términos de la sucesión ‘a₁’ y ‘a₂’ y vamos a comprobar si su suma es igual al resultado de sustituir la ‘n’ por ‘2’ en la ecuación del otro lado de la igualdad.
1² + 3² = ; 1² + 3² =
; 1 + 9 =
; 10 =
; 10 = 10
Vemos que también se cumple la ecuación para ‘n=2’.
Seguimos con las comprobaciones y vamos a probar si se cumple para ‘n=3’.
Tomamos los 3 primeros términos de la sucesión ‘a₁’, ‘a₂’ y ‘a₃’ y vamos a comprobar si su suma es igual al resultado de sustituir la ‘n’ por ‘3’ en la ecuación del otro lado de la igualdad.
1² + 3² + 5² = ; 1 + 9 + 25 =
; 35 =
; 35 =
; 35 = 35
También se cumple la ecuación para ‘n=3’.
3º - Realizamos una hipótesis sobre el cumplimiento de la ecuación para ‘n’.
Podríamos seguir probando con los distintos valores de ‘n’, pero si se ha cumplido para n=1, n=2 y n=3, podemos suponer que se cumple para ‘n’.
4º - Comprobamos si la ecuación también se cumple para valores mayores que ‘n’ y para ello vamos a probarlo con ‘n+1’.
En uno de los lados de la igualdad tenemos una suma de ‘n’ números impares al cuadrado. Para realizar la comprobación con ‘n+1’ tenemos que añadir un sumando más, que será el resultado de sustituir en el último término (2n-1) ² el valor de la ‘n’ por ‘n+1’.
En el otro lado de la igualdad, tenemos una ecuación donde hay que sustituir el valor de ‘n’ por ‘n+1’.
1² + 3² + 5² + 7² + 9² +…………..+ (2n-1)² + (2(n+1)-1)² =
 |  |  | |||
| + (2(n+1)-1)² | = |
Realizamos operaciones en cada lado de la igualdad para reducir al máximo las expresiones.
Primero quitamos los paréntesis internos:
Seguimos operando para eliminar todos los paréntesis:
Aplicamos la igualdad notable (a + b)²= a²+2ab+b:
|
Realizamos la multiplicación
Sustituimos el resultado y seguimos operando.
Calculamos el mcm (mínimo común múltiplo) para que todo tenga el mismo denominador y seguimos realizando operaciones.
m.c.m. = 3
| = | |||
| Son iguales. |
Hemos comprobado que también se cumple para ‘n+1’.
Por el Principio de la Inducción, podemos asegurar que se cumple la igualdad.
Resuelto por Blanca Minguito.
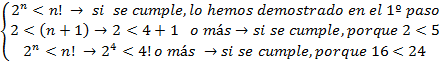
![clip_image002[12] clip_image002[12]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjZSmgvRj-q3T1MdERgt1odDRZYC08PrqR6XTPsRcDl8w8xe-dDCZg6Ou-9aVQTE4tE4wHCgWmnhxb9wjHIvrW0eA4ZHtL38BJGuGU0oZM5HchsH-NeVHk2H1x6aC_wbqeC1TowUV3AHVFt/?imgmax=800)